CHAPTER 7 DEFINITION OF IMPORTANT ABBREVIATIONS
CHAPTER 7 DEFINITION OF IMPORTANT ABBREVIATIONS
บทที่ 7
ความหมายของคำย่อที่สำคัญ
DEFINITION OF IMPORTANT ABBREVIATIONS
ในเรื่องเคโมเมทริกมีพารามิเตอร์ทางสถิติจำนวนมากที่ใช้สำหรับการบ่งชี้สมรรถนะของวิธีการต่างๆ ความรู้ในรายละเอียดของสูตรต่างๆโดยทั่วไปแล้วไม่จำเป็นสำหรับการคำนวณหรือการหาแบบจำลองที่ดีที่สุดในการวิเคราะห์แบบเชิงปริมาณ อย่างไรก็ดีบทที่ 7 นี้ให้ความหมายทางคณิตศาสตร์ของตัวย่อที่ใช้กันทั่วไปเพื่อช่วยผู้อ่านในการศึกษาบทความเฉพาะ
b-Coefficient สัมประสิทธิ์ b: ดู Calibration function ฟังก์ชั่นคาลิเบรชั่น
Bias ความผิดพลาดเฉลี่ย: โดยทั่วไป Bias เป็นความแตกต่างเฉลี่ยของชุดข้อมูลที่วัดจริงกับค่าทำนาย การคำนวณทำโดยหาค่าเฉลี่ยของค่าความแตกต่างของตัวอย่างทุกๆตัวอย่างในชุดข้อมูลดังสมการ

Bias Correction การแก้ไขความผิดพลาดเฉลี่ย: เพื่อที่จะใช้แบบจำลองกับเครื่องสเปกโตรมิเตอร์ที่แตกต่างกันหรือที่สถานที่ต่างกัน บางทีต้องมีการปรับค่าก่อนที่แบบจำลองจะถูกใช้อย่างเต็มรูปแบบ ถ้าตัวอย่างที่เหมือนกันถูกวัดที่ห้องปฏิบัติการต่างกันแต่ใช้สเปกโตรมิเตอร์ชนิดเดียวกันจะพบว่าได้ค่าที่แตกต่างกัน ความผิดพลาดเฉลี่ย (Bias) ในกรณีนี้ เป็นกรณีของการเปลี่ยนแปลงสถานที่วัด ซึ่งค่าเบี่ยงเบนที่เป็นระบบ (Systematic deviations) ของค่าอ้างอิงของห้องปฏิบัติการที่แตกต่างกัน เมื่อมีการเปลี่ยนแปลงจากเครื่องวัดหนึ่งไปยังอีกเครื่อง แม้แต่การเปลี่ยนแปลงที่น้อยที่สุดระหว่างสเปกโตรมิเตอร์ ก็สามารถนำไปสู่สเปกตรัมที่ต่างกัน การปรับค่าวิเคราะห์ดั้งเดิมเป็นค่าใหม่ที่คาดหวัง จะต้องลบความแตกต่าง (คือความผิดพลาดเฉลี่ย (bias)) จากค่าทำนาย วิธีการนี้แบบจำลองที่มีอยู่จะสามารถใช้ที่สถานที่วัดต่างๆหรือเครื่องมือที่ต่างไปได้
ไม่ควรจะสับสนระหว่างการแก้ไขความผิดพลาดเฉลี่ย (bias) กับการแก้ไข Offset และ Slope (Offset and Slope correction) ในที่นี้ค่าที่ถูกทำนาย ถูกพล็อตเทียบกับค่าจริง และเส้นรีเกรสชั่น (regression) จะถูกคำนวณ ซึ่งการแก้ไขนี้ปรับเส้นรีเกรสชั่น (regression) ให้อยู่แนวเส้นแบ่งครึ่ง (bisector) (เส้น 45 องศา) เพื่อที่ว่าโดยเฉลี่ยค่าทำนายใหม่และค่าดั้งเดิมจะเท่ากัน (สำหรับรายละเอียดเพิ่มเติมดูได้ที่การแก้ไข Offset และ Slope)
โดยทั่วไปหาก Slope (ความชัน) ของเส้นรีเกรสชั่น เป็น “1” หรือใกล้กับ “1” ค่า offset หรือค่าตัดแกน Y จะเท่ากับค่าเบี่ยงเบนเฉลี่ยเชิงระบบของค่าทำนายจากค่าดั้งเดิม (ค่าวัดจริง) (คือ bias) ดังนั้นปกติ Offset และ Bias แทบจะเหมือนกัน ในบทความต่างๆ มักจะเรียกว่า “การแก้ไขความผิดพลาดเฉลี่ยและความชัน (Bias and Slope correction)” แม้ว่าที่จริง offset ของเส้นรีเกรสชั่น ถูกนำไปใช้สำหรับการแก้ไข อย่างไรก็ตาม ถ้าไม่มีความสัมพันธ์เชิงเส้นระหว่างค่าดั้งเดิมและค่าทำนาย ความชันของเส้นรีเกรสชั่นที่ได้จะแตกต่างจาก “1” ความผิดพลาดเฉลี่ยและ Offset (Bias and Offset) จะแตกต่างกันและการแก้ไขความผิดพลาดเฉลี่ย (bias correction) จะนำไปสู่ค่าที่แตกต่างกันเมื่อเปรียบเทียบกับการแก้ไข offset
Calibration Function ฟังก์ชั่นคาลิเบรชั่น: ในระหว่างการคาลิเบรชั่น (Calibration) หรือการสร้างแบบจำลอง จะวัดตัวอย่างที่ทราบความเข้มข้นแล้วจำนวนหนึ่ง ฟังก์ชั่นคาลิเบรชั่น b (Calibration Function b) จะสร้างความสัมพันธ์ระหว่างสมบัติ Y (ตัวอย่างเช่น ความเข้มข้นของสารที่วิเคราะห์) กับค่าการทดลอง X (ตัวอย่างเช่น สเปกตรัม (spectrum))
b = (XT•X)-1•XT•Y (7-2)
X และ Y ถูกเขียนในรูปแบบเมทริกซ์ ในบทความของผู้เชี่ยวชาญมักจะเรียกฟังก์ชั่น b ว่า b-coefficient หรือค่าสัมประสิทธิ์รีเกรสชั่น (regression coefficient) จากฟังก์ชั่นนี้ทำให้สามารถคำนวณความเข้มข้นวิเคราะห์ได้โดยตรงจากสเปกตรัม (spectrum) (ขั้นตอนอธิบายไว้ในบทที่ 2 และ 3)
Y = X ∙ b (7-3)
นักพัฒนาวิธีการที่มีประสบการณ์มักจะสังเกตค่าสัมประสิทธิ์ b ของการคาลิเบรชั่นเพื่อที่จะหาช่วงสเปกตรัมที่เหมาะสมสำหรับการพัฒนาแบบจำลอง ช่วงเหล่านี้ของสเปกตรัมซึ่งมีข้อมูลที่สำคัญของสารที่วิเคราะห์มักจะมีส่วนสำคัญต่อค่าสัมประสิทธิ์รีเกรสชัน
Coefficient of Determination ค่าสัมประสิทธิ์ของการพิจารณา: ดู R2
Correlogram คอร์เรโลแกรม: Correlogram แสดงระดับความสอดคล้องระหว่างข้อมูลเชิงสเปกตรัมกับความเข้มข้นสำหรับจำนวนแฟคเตอร์ใดๆ ค่าที่เข้าใกล้ +1 หรือ -1 แสดงว่าข้อมูลสเปกตรัมช่วงเหล่านั้นมีความสัมพันธ์ที่ดีเกิดขึ้น ส่วนค่าที่ใกล้ 0 แสดงว่ามีความสัมพันธ์ไม่เพียงพอ ช่วงนี้ไม่ควรใช้สำหรับการคาลิเบรชั่น
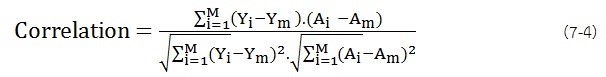
Differ ค่าความแตกต่าง: คือความแตกต่างระหว่างค่าความเข้มข้นของตัวอย่าง i ที่วัดจริงและ ค่าที่ได้จากการทำนาย
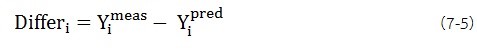
Error of Analysis ความคลาดเคลื่อนของการวิเคราะห์: ดู Error of Prediction ความคลาดเคลื่อนของการทำนาย
Error of Prediction ความคลาดเคลื่อนของการทำนาย: คุณภาพของการคาลิเบรชั่นโดยปกติพิจารณาจากความแม่นยำในการวิเคราะห์ตัวอย่างใหม่ที่ไม่รู้ ซึ่งตรวจสอบระหว่างการพัฒนาวิธีการ (แบบจำลอง) ในที่นี้ความคลาดเคลื่อนในการวิเคราะห์เฉลี่ยโดยรวมถูกคำนวณสำหรับตัวอย่างทั้งหมด ค่านี้เรียกว่า RMSECV (ดูข้างล่าง) สำหรับการพิสูจน์ภายใน และ RMSEP (ดูข้างล่าง) สำหรับการพิสูจน์ภายนอก
Explained Variance ความแปรปรวนที่อธิบายได้: ดู R2
Factor แฟคเตอร์: เมทริกซ์ของข้อมูลความเข้มข้นและเมทริกซ์ของข้อมูลสเปกตรัม ถูกแบ่งออกเป็นคู่ของเวคเตอร์ของ scores และ loadings โดยขั้นตอน PLS (ดูสมการ 2-3 และ 2-4) แต่ละคู่ของเวคเตอร์ของ scores และ loading เรียกว่า แฟคเตอร์
FValue และ FProb: F-Value ถูกใช้สำหรับการระบุความผิดปกติ (Outlier) ในชุดข้อมูลคาลิเบรชั่น ซึ่ง F-Value โดยทั่วไปแล้วได้จากค่าเชิงสเปกตรัมและค่าความเข้มข้น (concentration) ของตัวอย่างที่ถูกวัด F-Value มี 2 ชนิด คือ ค่าซึ่งถูกคำนวณได้โดยตรงจากค่าที่สเปกตรัมอธิบายไม่ได้ (Spectral Residuae) และค่าที่เป็นผลจากความแตกต่างของค่าจริงและค่าที่ถูกทำนาย (ถูกทำนายโดยแบบจำลองทางเคโมเมตริกซ์) F-Value ของตัวอย่างที่วิเคราะห์ยิ่งมาก เป็นได้อย่างมากที่จะเป็นความผิดปกติ (Outlier)
การคำนวณ F-Value สำหรับการหาความผิดปกติของสเปกตรัม
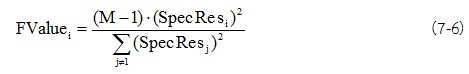
การคำนวณ F-Value สำหรับการหาความผิดปกติของค่าความเข้มข้น (Concentration)
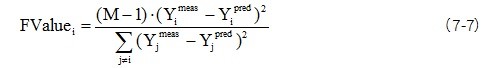
F-Value ที่ผิดปกติของค่าความเข้มข้น สามารถคำนวณได้จากความแตกต่างระหว่างค่าที่ถูกวัดและค่าของตัวอย่างที่ถูกทำนาย i ซึ่ง M คือ จำนวนตัวอย่างในชุดข้อมูลคาลิเบรชั่น
ค่าและการกระจายตัวของ F-Value ขององค์ประกอบหนึ่งชนิดขึ้นอยู่กับการประยุกต์ใช้ เพื่อที่จะตัดสินว่า F-Value อาจจะบ่งชี้ความผิดปกติได้หรือไม่ มันจะต้องถูกเปรียบเทียบกับ F-Value ของตัวอย่างอื่นๆ ของชุดข้อมูล เพราะฉะนั้นจึงต้องคำนวณ FProb Value ค่านี้บ่งชี้ความเป็นไปได้ของการมีอยู่ของตัวอย่างผิดปกติในการกระจายตัวของ F-Value ทั้งหมด
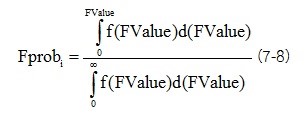
ถ้า F-Value เป็น 0 ทำให้ผลของ FProb เป็น 0 (นั่นคือ ความเป็นไปได้ที่ตัวอย่างนั้นจะเป็นตัวอย่างผิดปกติเป็น 0 %) มีทางเป็นไปได้น้อยมากที่ F-Value มากแล้วนำไปสู่ FProb เป็น 1 (นั่นคือ ความเป็นไปได้ 100 %)
Leverage: leverage คือ ค่าที่ใช้แสดงอิทธิพลของตัวอย่างต่อแบบจำลอง PLS ในทางคณิตศาสตร์ leverage คือ ระยะมาฮาลาโนบิส (Mahalanobis distance) ของตัวอย่างใดๆในชุดสร้างแบบจำลอง (ดู Mahalanobis distance) ค่า leverage สำหรับค่าที่ผิดปกติจะมีค่าสูงอย่างผิดปกติเมื่อเทียบกับตัวอย่างอื่น
Mahalanobis distance ระยะมาฮาลาโนบิส: ในระหว่างการสร้างแฟคเตอร์ สเปกตรัมของตัวอย่างที่วัดจะถูกแยกส่วนเป็นแฟคเตอร์ต่างๆและค่าที่สเปกตรัมอธิบายไม่ได้ (Spectral Residual) (ดูสมการ 2-3) ซึ่งใช้ได้ทั้งตัวอย่างชุดคาลิเบรชั่นกับตัวอย่างชุดพิสูจน์ ถ้าวิเคราะห์ตัวอย่างที่ไม่รู้ค่าโดยใช้แบบจำลอง PLS ควรจะเช็คว่าสามารถวิเคราะห์สเปกตรัมได้อย่างถูกต้องโดยใช้วิธีนี้ ซึ่งทำได้โดยการคำนวณระยะมาฮาลาโนบิส ในที่นี้คือเป็นการเช็คว่าสเปกตรัมของตัวอย่างนั้น “fits” สเปกตรัมต่างๆของข้อมูลชุดสร้างแบบจำลอง
ระยะมาฮาลาโนบิส ถูกกำหนดนิยามว่าเป็นความแตกต่างของสเปกตรัมของตัวอย่างที่วัดจากค่าสเปกตรัมเฉลี่ยของสเปกตรัมทั้งหมดในชุดสร้างแบบจำลอง ซึ่งถูกใช้เมื่อสร้างเมทริกส์ของสเปกตรัมของชุดตัวอย่างที่ต้องการวัดขึ้นมาใหม่ เมื่อความแตกต่างมากขึ้น ค่าระยะมาฮาลาโนบิสก็มากขึ้น มีเหตุผลที่เป็นไปได้หลายอย่าง เช่นการรบกวนจากภายนอก เช่น การปนเปื้อนของตัวอย่างหรือการรบกวนที่เกิดจากการเปลี่ยนแปลงของอุณหภูมิ ซึ่งจะนำไปสู่การบิดเบือนของพีค ซึ่งมีผลทำให้ระยะมาฮาลาโนบิสเพิ่มขึ้น ในทำนองเดียวกัน ค่านี้จะเพิ่มขึ้นถ้าตัวอย่างที่วิเคราะห์มีค่าความเข้มข้นนอกช่วงของชุดคาลิเบรชั่น ระยะมาฮาลาโนบิสเป็นการวัดเชิงปริมาณของความน่าเชื่อถือในการวิเคราะห์ เพราะตัวอย่างที่ผิดปกติ (outliers) หรือตัวอย่างที่มีค่าอ้างอิงนอกช่วงจะถูกตรวจพบ
ขณะที่ทำ PLS Regression (สร้างแบบจำลอง) จะมีการคำนวณระยะมาฮาลาโนบิสของสเปกตรัมของตัวอย่างทุกๆตัวอย่าง จากผลที่ได้เหล่านี้ค่าสูงสุดที่ยอมรับได้จะถูกคำนวณเพื่อสเปกตรัมของตัวอย่างจะถูกวิเคราะห์ได้อย่างปลอดภัยด้วยแบบจำลองนั้น ตัวอย่างที่มีค่าระยะมาฮาลาโนบิสสูงกว่านี้ (ค่าสูงสุดที่ยอมรับได้) จะไม่น่าเชื่อถือ ตัวอย่างเหล่านี้มีแนวโน้มที่จะเป็นตัวอย่างผิดปกติหรือนอกกลุ่ม (outliers)
ถ้าข้อมูลสเปกตรัมถูกแปลงเป็นแฟคเตอร์ตามสมการ (2-3) ระยะมาฮาลาโนบิส hi จะถูกคำนวณดังนี้
hi = tiT(XT•X)-1 • ti (7-9)
เมื่อมีการคำนวณหาแฟคเตอร์จำนวน R แฟคเตอร์ ถ้า Score vector (ti) ไม่ได้ถูกคำนวณจากตัวอย่างที่ไม่ทราบค่า (Unknown sample) แต่ถูกคำนวณจากสเปกตรัมในชุดคาลิเบรชั่น (Calibration spectrum) ซึ่งเรียกว่า “Leverage” ค่า Leverage ของตัวอย่างชุดคาลิเบรชั่น เป็นค่าที่แสดงอิทธิพลของตัวอย่างต่อแบบจำลอง PLS
MDL (Minimum Description Length): เป็นค่าที่ได้จากการทดลองซึ่งกำหนดจำนวนที่เหมาะสมของแฟคเตอร์
MDL = M ln (SSE/M) + R ln M (7-10)
Offset- and Slope Correction การแก้ไขออฟเซตและการแก้ไขความชัน: การแก้ไขออฟเซตเป็นการปรับค่าของเส้นรีเกรสชั่น เป็นค่าเดิมโดยลบค่าออฟเซต (นั่นคือ ระยะที่กราฟตัดแกน y) จากจุดต่างๆบนกราฟ
การแก้ไขออฟเซตและการแก้ไขความชันมีความสำคัญในสเปกโทรสโคปีสำหรับการย้ายแบบจำลอง (Calibration transfer) จากเครื่องวัด (Spectrometer) หนึ่งไปยังเครื่องวัดอื่น วิธีการ (แบบจำลอง) ถูกติดตั้ง (สร้าง) บนเครื่องที่เป็นศูนย์กลาง หรือเครื่องวัดหลัก “Master” วิธีการนี้สามารถถูกนำมาใช้กับเครื่องวัดอื่นๆที่เป็นบริวาร “Slaves” ของเครื่องวัดหลัก การเปลี่ยนแปลงเชิงระบบเฉพาะเครื่องบริวารจะถูกคำนวณกลับเป็นค่าที่คาดหวังสำหรับระบบเครื่องหลักด้วยค่าแก้ไขที่เหมาะสม เครื่องวัดนั้นจะกำหนดค่ามาตรฐานให้กับทุกๆค่าการวัดที่มีความสัมพันธ์กัน การประเมินผลของเครื่องสเปกโตรมิเตอร์ที่เป็นบริวารสามารถดำเนินการได้เหมือนเครื่องสเปกโตรมิเตอร์หลัก นี้เป็นการอธิบายสั้นๆสำหรับการคาลิเบรชั่นแบบหลายตัวแปร (Multivariate calibration)11
สเปกตรัมซึ่งถูกสร้างขึ้นโดยเครื่องวัดหลักและเครื่องบริวารระหว่างทำการวัดตัวอย่างชุดเดียวกันถูกอ่านอยู่ในรูปเมทริกซ์ข้อมูลสเปกตรัม MX คือ เมทริกซ์ข้อมูลสเปกตรัมของเครื่องวัดหลัก sX คือ เมทริกซ์ข้อมูลสเปกตรัมของเครื่องวัดบริวาร จากการทราบค่าความเข้มข้นของตัวอย่างชุดคาลิเบรชั่น ค่าสัมประสิทธิ์การถดถอย Mb จะถูกคำนวณซึ่งเชื่อมโยงข้อมูลสเปกตรัมและข้อมูลความเข้มข้นสำหรับการวัดของเครื่องวัดหลัก โดยเปรียบเทียบกับสมการ (2-1)
MY = MX · Mb ( 7-11)
สำหรับการวัดด้วยเครื่องมือบริวาร ไม่มีการดำเนินการคาลิเบรชั่นเพิ่มเติม
สำหรับการวัดเครื่องมือรองพวกเขาจะเชื่อมโยงกับค่าสัมประสิทธิ์ Mb ซึ่งถูกสร้างขึ้นจากเครื่องมือหลัก:
SY=SX . Mb
ถ้าเครื่องมือหลักและเครื่องมือรองผลิตสเปกตรัมเหมือนกัน (MX=SX)ผลการวิเคราะห์มีความเท่าเทียมกันสำหรับทุกกรณี (MY=SY)คือการวัดตัวอย่างที่สามารถดำเนินการที่ใช้ในการใดๆนี้เป็นกรณีที่มีความแม่นยำสูง FT-spectrometers
ถ้าเครื่องมือหลักและเครื่องมือรองสร้างสเปกตรัมที่แตกต่างกันจากตัวอย่างที่เหมือนกันอย่างใดอย่างหนึ่งจะพยายามที่จะปรับความเข้าใจกับการแก้ไข offset/slope สำหรับการคาดการณ์ปริมาณความเข้มข้นของเครื่องมือรอง ค่าจริงที่สอดคล้องกันของเครื่องมือรองที่มีพล็อตที่ได้รับการพิจารณาที่มีการวัดตัวอย่างเพิ่มเติม
ในกรณีที่ผลการวัดที่เหมือนกันของทั้งสองปัญหาที่ได้จากค่า Y-เดียวจะทำให้เส้นแบ่งครึ่ง ขณะที่เครื่องมือหลักและเครื่องมือรองสร้างสเปกตรัมที่แตกต่างกันในความเป็นจริงมีการเบี่ยงเบนจากเส้นแบ่งครึ่ง ดังนั้นระยะเวลาการแก้ไขการคำนวณที่แปลงเส้นถดถอยกำหนดเป็นเส้นแบ่งครึ่ง:
SYcorrected = (sx . Mb) - offset (7-13)
แต่ถ้าชดเชยและความชันของเส้นถดถอยจำเป็นต้องได้รับการแก้ไขจะเรียกว่าการแก้ไข offset/slope
SYcorrected=((sX . Mb) - offset) . slope-1 (7-14)
ความลาดชันและ Offset เป็นเงื่อนไขที่เกี่ยวข้องกับการแก้ไขซึ่งการคำนวณโดยตรงของความเข้มข้นของสารที่เป็นไปได้ การคำนวณของพวกเขาคือการอธิบาย ใน11
PRESS (ผลรวมข้อผิดพลาดการทำนายที่เหลือของสแควร์ส): ผลรวมของความผิดพลาดยกกำลังสองทั้งหมดของการทำนาย ค่านี้จะช่วยในการเพิ่มประสิทธิภาพของเวกเตอร์จำนวน PLS:
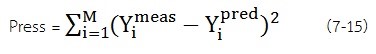
PWS (สเปกตรัม น้ำหนักคุณสมบัติ): PWS เป็นตัวนับของสมการ correlogram ค่า PWS สูง
ช่วงสเปกตรัมที่ไม่เพียงพอให้ทำเครื่องหมายไว้ซึ่งยังมีความสัมพันธ์ที่ดีของชุดข้อมูลที่สามารถพบได้ (เช่น correlogram) แต่ยังมีความเข้มของกลุ่มที่เพียงพอที่จะสามารถสังเกตเห็นได้ในการตั้งค่าวิธีการสอบเทียบช่วงสเปกตรัมกับ correlogram สูงและค่า RWS สูงควรจะเลือกใช้สมการที่ 7-16
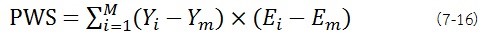
R2: การกำหนดค่าสัมประสิทธิ์ (R2) ให้ร้อยละของความแปรปรวนในปัจจุบันในค่าส่วนประกอบซึ่งมีการทำซ้ำในการทำนายค่าสัมประสิทธิ์นี้มักจะเรียกว่าอธิบายความแปรปรวนค่าสัมประสิทธิ์ที่สูงแสดงความสัมพันธ์ที่ดีขึ้นระหว่างข้อมูลความเข้มข้นและข้อมูลสเปกตรัม ถ้าต่ำกว่า R2 โดยทั่วไปนำไปสู่การวิเคราะห์ข้อมูลที่ไม่ดี มีเหตุผลที่เป็นไปได้ต่างๆสำหรับความสัมพันธ์ที่ไม่ดีเหล่านี้ : การเลือกพารามิเตอร์ที่ไม่เหมาะสมจะนำไปสู่ของการกำหนดค่าสัมประสิทธิ์ต่ำ (R2 « 90%) เช่นเดียวกับตัวอย่างที่มีความแม่นยำไม่เพียงพอของข้อมูลอ้างอิงหรือการมีอยู่ของค่าที่ผิดปกติในการกำหนดข้อมูลการสอบเทียบ
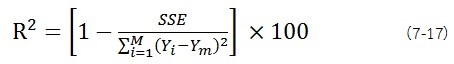
สัมประสิทธิ์การถดถอย : ดูฟังก์ชันการสอบเทียบ
Rank: หมายเลขของปัจจัย PLS
วัสดุตกค้าง : ตัวประกอบไม่สามารถอธิบายความแปรปรวนรวมของข้อมูลที่มีความเข้มข้นหรือเมทริกซ์ข้อมูลสเปกตรัมได้ ส่วนที่เหลือที่ไม่ได้อธิบายได้ด้วยตัวประกอบเรียกว่าวัสดุตกค้าง ; ค่าตามลำดับของค่าที่เหลือ (ดูสมการ 2-3 และ 2-4) วัสดุตกค้างคือความแตกต่างระหว่างข้อมูลจริงและข้อมูลที่สร้างขึ้นใหม่โดยตัวประกอบ ซึ่งนำไปใช้กับข้อมูลสเปกตรัมเช่นเดียวกันกับข้อมูลที่มีความเข้มข้น มีจำนวนของวัสดุตกค้าง ซึ่งเป็นที่สนใจใน chemometrics เช่น เป็นมูลค่าคงเหลือของสเปกตรัมที่เหลือเมทริกซ์ F (ดูสมการ (2-4))
F = X - (t1p1T+t2p2T+t3p3T+…+tRpRT) (7-18)
ยิ่งค่านี้มีค่ามากขึ้น จะมีส่วนมีของโครงสร้างสเปกตรัมเพียงส่วนน้อย ซึ่งสามารถอธิบายด้วยวิธี Factorization
ในทำนองเดียวกัน เมทริกซ์ของความผิดพลาด (Residual metrix) ของข้อมูลความเข้มข้น G อธิบายถึงส่วนขององค์ประกอบของข้อมูลชุดคาลิเบรชั่นที่ไม่สามารถอธิบายได้ด้วยวิธี Factorization

การคำนวณค่าความผิดพลาดจะเป็นประโยชน์ไม่เพียงแต่สำหรับการประเมินแบบจำลอง ค่าความผิดพลาดของสเปกตรัมของตัวอย่างเป็นเบาะแสสำคัญสำหรับการตรวจสอบค่าผิดปกติ (Outlier) ในที่นี้ ความแตกต่างที่คำนวณได้ระหว่าง xi สเปกตรัมวัดและ si สเปกตรัมซึ่ง "คาดว่า" ได้จาก Factorization:
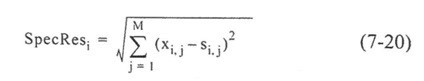
ผลรวมถูกคำนวณที่ทุกค่าความถี่ (ดัชนี "j") xi เป็นสเปกตรัมที่วัด และ si เป็นสเปกตรัมรวม:
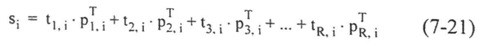
ยิ่งค่าความผิดพลาดมีค่ามาก (นั่นคือ ความแตกต่างระหว่างสเปกตรัมจริงและสเปกตรัมจาก Factorization มีค่ามาก) แนวโน้มที่ตัวอย่างเป็นค่าผิดปกติยิ่งมาก ในวิธีนี้ การปนเปื้อนในสเปกตรัมสามารถตรวจพบ ซึ่งซ้อนทับยอดของสเปกตรัมของตัวอย่างและนำไปสู่การเพิ่มขึ้นของค่าความผิดพลาด นอกจากนี้ค่านี้มักจะใช้สำหรับการกำหนดค่าผิดปกติ นอกเหนือจากการคำนวณระยะ Mahalanobis
RMSECV (Root Mean Square Error of Cross Validation): ค่านี้เป็นค่าเชิงปริมาณสำหรับระบุความแม่นยำซึ่งตัวอย่างต่างถูกทำนายระหว่างการพิสูจน์ RMSECV เทียบได้กับ RMSEP ของการพิสูจน์ภายนอก
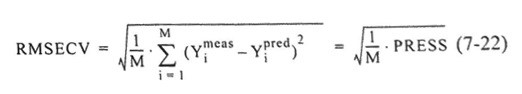
RMSEE: (Root Mean Square Error of Estimation) ค่านี้คำนวณความผิดพลาดของการวิเคราะห์ของแบบจำลอง
ข้อควรระวัง RMSEE ไม่เหมาะสำหรับการพิสูจน์เนื่องจากไม่มีสเปกตรัมชุดทดสอบอิสระที่ใช้ในการพิสูจน์ ดูบทที่ 6-C
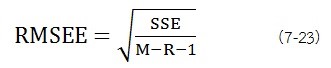
RMSELC (Root Mean Square Error of Leverage Correction) ค่านี้ถูกคำนวณระหว่างการคาลิเบรชั่นซึ่งเป็นค่าประมาณขนาดของความคลาดเคลื่อนที่คาดไว้ของการวิเคราะห์ตัวอย่างที่ไม่รู้ชุดใหม่
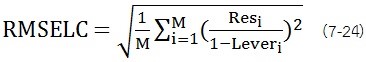
RMSEP (Root Mean Square Error of Prediction) ค่านี้เป็นค่าเชิงปริมาณสำหรับบ่งบอกความแม่นยำของการวิเคราะห์ตัวอย่างชุดทดสอบ ซึ่งเปรียบได้กับค่า RMSECV ของการพิสูจน์แบบภายใน
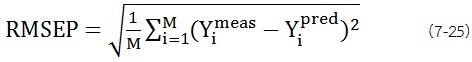
RPD (Residual Prediction Deviation) ค่า RPD เป็นเศษส่วนของค่าเบี่ยงเบนมาตรฐานของค่าอ้างอิง (SD) และค่าความคลาดเคลื่อนเฉลี่ยแบบแก้ไข bias ของการทำนายของชุดพิสูจน์ (SEPbias)

เมื่อ 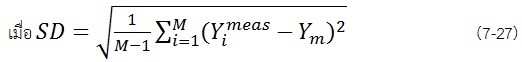
และ
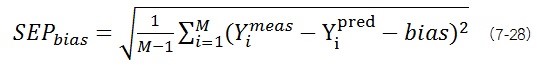
เป็นค่าเชิงคุณภาพสำหรับการประเมินผลการพิสูจน์ ยิ่ง มีค่าน้อยเมื่อเปรียบเทียบกับความแปรปรวนของค่าอ้างอิง แบบจำลองยิ่งให้ผลดี นั่นคือยิ่งค่าRPD ยิ่งมาก การคาลิเบรชั่นจะยิ่งดี
เพื่อที่จะวิเคราะห์คุณภาพของการพิสูจน์ การคำนวณ RPD มีความหมายมากกว่าการดูเฉพาะความคลาดเคลื่อนของการทำนาย ตัวอย่างเช่น ในการพิสูจน์แบบจำลองที่มีช่วงแคบ มักจะทำให้ค่าการทำนายมีความคลาดเคลื่อนน้อย แบบจำลอง “รู้” เพียงความแปรปรวนเล็กน้อยในชุดข้อมูลที่ใช้อ้างอิง และจะทำนายค่าวิเคราะห์ด้วยความแปรปรวนน้อย (นั่นคือ มีความคลาดเคลื่อนเล็กน้อย) ถึงแม้ว่าแบบจำลองไม่ค่อยดี เพื่อหลีกเลี่ยงการแปลผลดีเกินไป (Over-optimistic interpretation) จึงมีการคำนวณค่า RPD โดยวิธีนี้จะทำให้เห็นว่าความเบี่ยงเบนมาตรฐาน (SD) ของค่าอ้างอิงมีค่าน้อย (low SD values) และแม้ว่าค่าความคลาดเคลื่อนของการทำนายเลวลงเพียงเล็กน้อย (growing values for SEPbias) จะนำไปสู่ค่า RPD ที่เลวลงอย่างชัดเจน ดังนั้นแม้ค่าความคลาดเคลื่อนของการทำนายเล็กน้อยอาจส่งผลให้แบบจำลองไม่ดีก็ได้ ซึ่งชี้วัดโดยใช้ค่า RPD
RPD มีข้อดีอย่างอื่นอีก: ดังที่เคยถูกกล่าวมาแล้วว่าตัวอย่างชุดคาลิเบรชั่นควรมีช่วงครอบคลุมช่วงคาริเบชั่นทั้งหมดอย่างสม่ำเสมอ แบบจำลองที่มีตัวอย่างจำนวนมากในช่วงกลางแต่มีเพียงสองสามตัวอย่างในตอนท้ายของช่วง (ดังรูปที่ 5.1) จะมีความครอบคลุมน้อย (less robust) สิ่งนี้เกี่ยวข้องกับ RPD ยิ่งการกระจายของค่าอ้างอิงสม่ำเสมอมากเท่าไร ก็จะยิ่งทำให้ค่าเบี่ยงเบนมาตรฐานสูงมากกว่าการจับกลุ่มอยู่ที่ตำแหน่งเดียว ยิ่ง RPD มาก แบบจำลองจะถูกจัดว่าดี
สำหรับเหตุผลในอดีต ค่า RPD ถูกใช้บ่อยในตลาดการเกษตร ตัวอย่างเช่น ในการวิเคราะห์ทางเนียร์อินฟราเรดสเปกโทรสโกปีของข้าวสาลี กฎทั่วไปเพื่อประเมินคุณภาพของคาลิเบรชั่นดังนี้
RPD ระหว่าง 2.5-3: วิธีการนี้ OK สำหรับการคัดกรองแบบหยาบๆ
RPD มากกว่า 3: วิธีการนี้ OK สำหรับการคัดกรอง
RPD มากกว่า 5: วิธีการนี้ OK สำหรับการควบคุมคุณภาพ
RPD มากกว่า 8: วิธีการนี้ดีมาก สำหรับงานวิเคราะห์ทุกๆงาน
ค่าเหล่านี้จะขึ้นอยู่กับชนิดของตัวอย่างและช่วงของชุดคาลิเบรชั่น
กฎที่กล่าวไว้ข้างต้น ควรจะถูกนำมาประยุกต์ใช้ในอุตสาหกรรมอาหาร (สำหรับตัวอย่างของแข็งเนื้อไม่สม่ำเสมอเป็นธรรมชาติ) สำหรับการวิเคราะห์ทางเคมี (ตัวอย่างของเหลวเนื้อสม่ำเสมอเป็นสารสังเคราะห์) การคาลิเบรชั่นควรมีค่า RPD ที่สูงกว่านี้
ค่า RPD เป็นค่าที่มีความสำคัญเช่นเดียวกับค่าความแปรปรวนที่อธิบายได้ “Explained variance” หรือ R2
ค่า R2 ยังช่วยในการประเมินผลเชิงคุณภาพของความคลาดเคลื่อนของการทำนายระหว่างที่พิสูจน์สมการ
สำหรับการคาลิเบรชั่นที่ไม่มีการปรับค่า bais (bais = 0) ใช้ความสัมพันธ์ต่อไปนี้
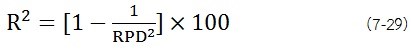
สำหรับ bias correction ที่มีค่าน้อย สมการนี้ใช้ประมาณค่าได้
SECV (Standard Error of Cross Validation) ค่าความคลาดเคลื่อนมาตรฐานในการพิสูจน์แบบไขว้: ดู RMSECV
SEE (Standard Error of Estimation) ค่าความคลาดเคลื่อนมาตรฐานในการประมาณ : ดู RMSEE
SEP (Standard Error of Prediction) ค่าความคลาดเคลื่อนมาตรฐานในการทำนาย : ดู RMSEP
Spectral Residuum : ดู Residuum
Slope Correction : ดู Bias Correction
SSE (Sum of Square Errors) ผลรวมกำลังสองของความคลาดเคลื่อน: ค่านี้ คือ ผลรวมของกำลังสองของค่า Residuum ค่า SEE ที่ได้ที่มากขึ้นแบบจำลองจะการอธิบายความแปรปรวนของชุดข้อมูลได้ยิ่งเลว
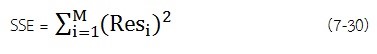
[1] “The copyright is belong to Dr. Jörg-Peter Conzen”
30 กันยายน 2561
ผู้ชม 4493 ครั้ง
